Definitions of Energy - Energy is a quantitative property of a system that depends on the motion and interactions of matter and radiation within that system. That there is a single quantity called energy is due to the fact that a system’s total energy is conserved, even as,within the system, energy is continually transferred from one object to another and between its various possible forms.

A spring of force constant $200 \mathrm{N} {\mathrm{m}}^{-1}$ is cut into three parts of lengths in ratio $1: 2: 3$. The smallest spring is further cut into two parts of equal length. The force constant of the shortest spring formed will be

At $t=\frac{2T}{3}$ a particle is at $\frac{-A}{2}$ and moving towards mean position. Find the equation of SHM. Also find the speed at $\frac{T}{4}$

A particle performs S.H.M. with amplitude $A$. The speed of particle is doubled at the instant when it is at $\frac{A}{2}$distance from mean position. The new amplitude of the motion is

A body attached to a spring oscillates in horizontal plane with frequency$n$. Its total energy is $E$ If the velocity in he mean position is$v$, then the spring constant is

For particle $P$ revolving round the centre $O$ with radius of circular path $r$ and regular velocity $\omega$, as shown in below figure, the projection of $OP$ on the $x$-axis at time $t$ is

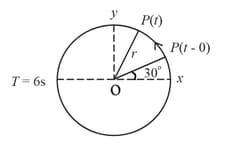
If initially a particle is at$x=\frac{-A}{\sqrt{2}}$ and its position is given by $x=A\cos \left(\omega t+\varphi \right)$ ) then find $\varphi$ if the particle is moving away from the mean position?

If velocity of body is half the maximum velocity. Then what is the distance from the mean position?

 A particle executes simple harmonic motion about $x=0$ along x-axis. The position of the particle at an instant is given by $x=(5 \mathrm{cm}) \mathrm{sin\pi t}$. Find the average velocity and average acceleration for a time interval $0$to $0.5 \mathrm{s}$.

 Two particles P and Q of equal masses are suspended from two massless springs of force constants $k_1$ and $k_2$ respectively. If maximum velocities during oscillation are equal then the ratio of amplitudes of P and Q is

The displacement of a particle executing simple harmonic motion is given by$y=A_0+A\sin \omega t+B\cos \omega t$.Then the amplitude of its oscillation is given by

 The equation of motion is represented by $y=\sin \omega t+\cos \omega t$. The time period of periodic motion is 

Two simple harmonic motions are represented by equations $y_1=4\sin (10t+\varphi )$ and $y_2=5\cos 10t.$ What is the phase difference between their velocities?
 

If the maximum velocity of a particle performing S.H.M. is $v$, then the average velocity during its motion from one extreme position to the other will be 

A body of mass $1 \mathrm{kg}$ is suspended from massless spring of natural length $1 \mathrm{m}$. If mass is released from rest, spring can stretch up to a maximum vertical distance of $40 \mathrm{cm}$, the potential energy stored in the spring at this extension is ($\mathrm{g}=10 {\mathrm{ms}}^{-2}$)

A block of mass $0.1 \mathrm{kg}$ attached to a spring of spring constant $400 {\mathrm{Nm}}^{-1}$ is pulled horizontally from$x = 0$ to $x_1 = 10 \mathrm{mm}$. Find the work done by spring force.
 

The work done by the tension in the string of a simple pendulum in one complete oscillation is equal to

Displacement of a particle is given by $y=0.2\sin \left(10\mathrm{\pi }t+1.5\mathrm{\pi }\right)$. Is it simple harmonic? If so, what is its period?

Two linear simple harmonic motions with same amplitude and frequency $\omega$ and $2\omega$ get superimposed on a particle in $x$ and $y$ direction. If the phase difference between the two are $\frac{\pi }{2}$ initially, the resultant path will be:

Equation of Displacement in SHM
The displacement $y\left(t\right)=A\sin \left(\omega t+\varphi \right)$ of a pendulum for $\varphi =\frac{2\pi }{3}$ is correctly represented by

Velocity of a particle moving along a straight line at any time $t$ is given by $v=\cos \left(\frac{\pi }{3}t\right)$. Find out the distance travelled by the particle in the first two seconds.